ROBERTO OSORIO

Roberto Osorio. Nacío en Mendoza, Argentina, el 8 de diciembre de 1953. Estudio Ingeniería Química y su primer trabajo fue en este campo: siete años en la Comisión Nacional de Investigación Científica.

En 1986 se radicó en Buenos Aires. y comenzó a trabajar directamente con empresas privadas en áreas de administración como consultor y ejecutivo.

Jugó ajedrez en su juventud. En 1998.decidíó asociarse al Club Argentino de Ajedrez de Buenos Aires. Descubrió allí, la «Peña del Mate de Ayuda», un grupo de problemistas que se reunen todos los sábados por la tarde. Desde entonces, este «hobby» ha sido parte de su vida. Disfruta mucho interactuando con sus amigos del ajedrez y comenta que le encantan las discusiones sobre el «sexo de los ángeles».

 

J. Lois & R. Osorio                  3°P. Die Schwalbe 2016  Proof game in 26.5 moves

J. Lois & R. Osorio               1ºP. Superproblem 2022    Proof game in 16.5 moves

R. Osorio & J. Lois             2º.P. Chanpagne 2023  Proof game in 25.0 moves

xxxxxxxxxxxxxx (xxxxxxx xxx

xxxxxxxxxxxxxx (xxxxxxx) xxx

xxxxxxxxxxxxxx (xxxxxxx) xxx

xxxxxxxxxxxxxx (xxxxxxx xxx

xxxxxxxxxxxxxx (xxxxxxx) xxx

xxxxxxxxxxxxxx (xxxxxxx) xxx

Soluc. Click en el Diagrama

PARTIDAS JUSTIFICATIVAS

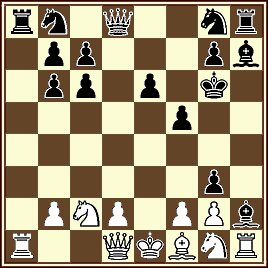
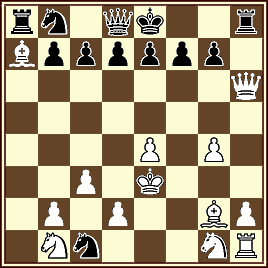
01 Jorge Lois – Roberto Osorio

1º Pr. StrateGems – 2009

Partida justificativa- en 23.0 jugadas

Tema: Sibling de sRR y doble Pronkin de wQ.

Solución:

1.e4 h5 2.Ag4 hxg4 3.c4 Th3 4.c5 Tc3 5.c6 dxc6 6.h4 Af5 7.h5 e6 8.h6 Ad6 9.h7 Ah2 10.h8Q g3 11.Qh5 Txc1+ 12.Qd1 Tc4 13.Qb3 Axe4 14.Qb6 axb6 15.a4 Ta5 16.Ca3 Th5 17.a5 Th8 18.a6 Ah7 19.a7 f5 20.a8Q Rf7 21.Qa4 Rg6 22.Qd1 Ta4 23.Cc2 Ta8

—————————————————————————————————–

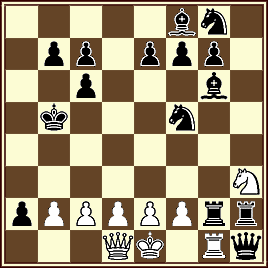
02 Roberto Osorio

3a. Hm. Problem Paradise-2003

Partida justificativa en 23,5 jugadas

Solución

1.g3 Cc6 2.Ag2 Cd4 3.Qc6 dxc6 4.Rf1 Qf5 5.Rg2 Ag6 6.Qf1 Cf5 7.Rf3 Rd7 8.Re4 Rd6 9.Rd3 Rc5+ 10.Rc3 Qd5 11.Qh3 Qxa2 12.Qxh7 Qxb1 13.Qh4 Qxc1 14.Qa4 Txh2 15.Ch3 Qxh1 16.Tg1 a5 17.Qa1 Rb5 18.Rb3 a4+ 19.Ra2 a3 20.Rb1 a2+ 21.Rc1 Ta3 22.Rd1 Txg3 23.Re1 Tgg2 24.Qd1

Circuito del Rey : (Re1–f1–g2-f3-e4-d3-c3-b3-a2-b1–c1–d1–e1)

Circuito de la Dama: (Qd1–f1–h3-h7-h4-a4-a1–d1), marcha real.

:—————————————————————————————————–

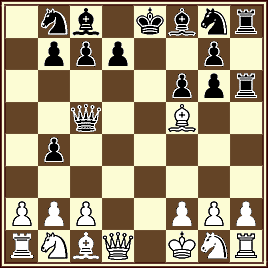
03 Roberto Osorio – Jorge Lois

“PCCC -Permanent Commission for Chess Composition-

Primer Premio –50th Anniversary Composing Festival” 2010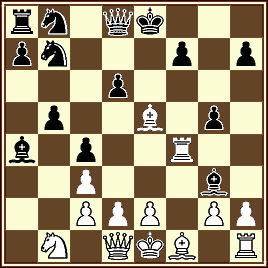

Solución

1.f4 Cf6 2.f5 Ce4 3.f6 Tg8 4.fxe7 Axe7 5.Ch3 Ah4+ 6.Cf2 g5 7.a4 Tg6 8.Ta3 Tc6 9.Tf3 Tc3 10.bxc3 c5 11.Aa3 c4 12.Ad6 Cc5 13.Ag3 d6 14.Ce4 Ad7 15.Tf2 Axa4 16.Ae5 b5 17.Cg3Cb7 18.Tf4 Axg3+

13+14 Proofgame en 18.0 C+

 

:—————————————————————————————————–

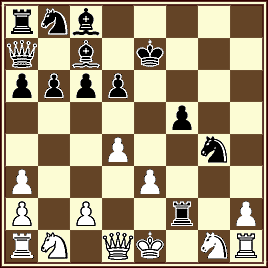
04 Jorge Lois & Roberto Osorio

6to. Premio

Solución

1.e4 a6 2.Ab5 axb5 3.d4 Ta6 4.d5 Th6 5.d6 f6 6.dxe7 Rf7 7.e8A+ Re7 8.Ag6 b4 9.Af5 Re8 10.e5 De7 11.e6 Dc5 12.e7 Rf7 13.e8A+ Re7 14.Ag6 hxg6 15.Rf1 Re8

Un certificado muy elegante y diseñado inteligentemente partiendo con un aparentemente simple posición final. Al principio sólo se ve 8 proyectos negros esenciales y evidentes y sólo tres del blanco. Entonces te das cuenta de que el Negro ha introducido dos tipos de bonos, y que el blanco también lo han hecho deben promover a sus peones perdidos. Ahí va repentinamente 2 * 6 jugadas blancas y de repente se fue todo y no es tan fácil ya. Dos löparförvandlingar blanco en e8 en torno a un rey negro hace su la mejor manera de mantenerse al margen de la forma , es a la vez divertido e impresionante.

:—————————————————————————————————-

05 Roberto Osorio & Jorge J. Lois

6th Prize StrateGems -2011

Solución

1.f4 a5 2.f5 a4 3.f6 a3 4.fxg7 f5 5.g4 Sf6 6.g8B Bh6 7.Bd5 Rg8 8.Bc6 dxc6 9.g5 Qd4 10.g6 Qa7 11.gxh7 Rg2 12.h8B Sg4 13.Bd4 Bf4 14.Bb6 cxb6 15.d4 Bc7 16.Bf4 Rf2 17.Bd6 exd6 18.e3 Ke7 19.Ba6 bxa6 20.bxa3. Very aesthetic problem. The main challenge resides in the need to organize a black piece to be captured on a3. As it can only be a pawn, we conclude that the black pawns on the sixth rank must all have captured, even though they look so unsuspicious. It turns out that we have two CF Bishops and both original Bishops captured. A finely composed problem.

PG 19½

:—————————————————————————————————-

06 Roberto Osorio & Jorge J. Lois

Rec. StrateGems -2011

Solución

1.c3 h5 2.Qa4 Rh6 3.Qxa7 Ra6 4.a4 Sc6 5.Qb8 Sf6 6.Qxc8 Sd5 7.Qb8 Sdb4 8.Qa7 Qb8 9.Qe3 Qa7 10.Qh6 0-0-0 11.Qh8 Qb8 12.Qxf8 Ra8 13.Qh8 Sa6 14.Qh6 Rh8 15.a5 Kd8 16.Ra4 Ke8 17.Rg4 hxg4 18.e4 g3 19.Ke2 gxf2 20.g4 Qd8 21.Bg2 Sab8 22.a6 f1S 23.a7 Sg3+ 24.Ke3 Se2 25.axb8B Sxc1 26.Ba7 Sb8.

Multiple siblings and circuits are shown in this problem, among other things. I can see the technical merit of it, but somehow I miss the aesthetics. Nonetheless, it is certainly a problem worth solving

PG 26

:—————————————————————————————————-